时间: 2025-08-18 05:46:19 来源: solidiq.chieffocus.com 作者: 财经动态
3、实验设计可信度的和数分析
(1)总体与样本
①总体:在统计学中,对于所考察的据处对象的全体,称为总体(或母体)。实验设计
②个体:组成总体的和数每个单元。
③样本(子样):自总体中随机抽取的据处一组测量值(自总体中随机抽取的一部分个体)。
④样本容量:样品中所包含个体的实验设计数目,用n表示。和数
例如,据处分析某河水总硬度,实验设计依照取样规则,和数从河中取来供分析用2000mL样品水,据处这2000mL样品水是实验设计供分析用的总体,如果从样品水中取出20个试样进行平行分析,和数得到20个分析结果(用x1,据处x2,x3…xi表示),则这组分析结果就是某河样品水的一个随机样本,样本容量为20。
(2)随机变量:来自同一总体的无限多个测量值都是随机出现的,叫随机变量。


(3)标准偏差
1)总体标准偏差(无限次测量)
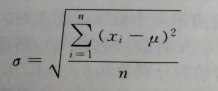

式中 n-----测量次数。
2)样本标准偏差(有限次测量)
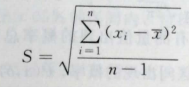
式中 n-1 -----自由度。
3)相对标准偏差

④标准偏差与平均偏差:当测定次数非常多(n大于20)时,δ=0.797 σ≈0.8σ,但是d-≠0.8S。
⑤平均值的标准偏差:统计学可证明平均值的标准偏差与单次测量结果的标准偏差存在下列关系:

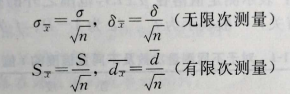
增加测定次数,可使平均值的标准偏差减少,但测定次数增加到一定程度时,这种减少作用不明显,因此在实际工作中,一般平行测定3~4次即可;当要求较高时,可适当增加平行测量次数。
4、随机误差的正态分布
(1)频数分布
①频数:每组中数据的个数。
②相对频数:频数在总测定次数中所占的分数。
③频数分布直方图:以各组分区间为底、相对频数为高做成的一排矩形。
④离散特性:测定值在平均值周围波动。波动的程度用总体标准偏差σ表示。
⑤集中趋势:向平均值集中。用总体平均值μ表示。在确认消除了系统误差的前提下,总体平均值就是真值。
(2)正态分布(无限次测量)
①正态分布曲线:如果以x--μ(随机误差)为横坐标,曲线最高点横坐标为0,这时表示的是随机误差的正态分布曲线。


记为:N(μ,σ2)
其中,μ决定曲线在X轴的位置,一决定曲线的形状。σ小则曲线高、陡峭,精密度好;σ大则曲线低、平坦,精密度差。
参考资料:食品检测技术,本文所用图片、文字版权归原作者所有。如涉及作品内容、版权等问题,请与本网联系。
相关链接:总硬度,样品,标准,曲线
《对于所考察的据处对象的全体》男孩、女孩宝宝名字推荐
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
·典范好文小教逝世朗读知乎感情故事2024/3/30三秒降泪的烦闷案牍
典范好文小教逝世朗读知乎感情故事2024/3/30三秒降泪的烦闷案牍http://www.hwenz.com/pic/典范好文小教逝世朗读知乎感情故事2024/3/30三秒降泪的烦闷案牍.jpg...
·人民日报评打差评被骚扰:网购物品不好,还不能给差评了?
人民日报评打差评被骚扰:网购物品不好,还不能给差评了?被各种商家营销套路侵害权益?买到的商品出故障投诉无门?黑猫投诉平台全天候帮您解决消费难题【消费遇纠纷,就上黑猫投诉】网购物品不好,还不能给差评了?百姓关注)本报记者秦瑞杰网购越来越普遍,许多人对网购行 ...
·观看人数最多5场勇士占3场 勇士回暖联盟赚翻
观看人数最多5场勇士占3场 勇士回暖联盟赚翻勇士在本季战绩回暖,目前以14胜2负高居联盟第一,让球迷也找回了熟悉的感觉,吸引他们重新回来观赛。据《SportsBusinessJournal》记者AustinKarp报道,本季在某知名美媒和TNT ...
·券商股全面飘红!行业总资产突破10万亿元,财富管理表现亮眼
券商股全面飘红!行业总资产突破10万亿元,财富管理表现亮眼11月22日,A股证券板块全面飘红!当天,券商股延续上周五的涨势,个股短线异动拉升。湘财股份(600095.SH)盘中涨停,截至收盘涨幅达7.69%,长城证券(002939.SZ)上涨4.76%,广发 ...
·阔别六年 「维多利亚的秘密」时装大秀盛大回归
阔别六年 「维多利亚的秘密」时装大秀盛大回归阔别六年,「维多利亚的秘密」Victoria's Secret)时装大秀终于在美国纽约市迎来了它的盛大回归。「维多利亚的秘密」时装大秀一直以其奢华的舞美设计、精致的服饰以及模特们的精彩演绎而闻名。本次 ...
·数据代码里隐藏“猫鼠游戏” 公司数据合规到底难在哪
数据代码里隐藏“猫鼠游戏” 公司数据合规到底难在哪原标题:数据代码里隐藏“猫鼠游戏”公司数据合规到底难在哪 公司数据合规到底难在哪数据代码里隐藏“猫鼠游戏”;数据出境存在法律间协调难点中国国家互联网应急中心发布的数据显示,2021年10月,网站安全方 ...
·韩媒:三星或于本周宣布在美芯片厂选址,总金额将达170亿美元
韩媒:三星或于本周宣布在美芯片厂选址,总金额将达170亿美元韩国《中央日报》11月22日报道,三星电子或将在本周于美国发布新的晶圆代工工厂投资计划,投资金额达到170亿美元。据三星电子21日透露,正在美国访问的李在镕19日前往白宫与拜登政府高层人士举行会谈。据 ...
·OPPO或2024年在印度推出电动汽车?相关人士:没听说过
OPPO或2024年在印度推出电动汽车?相关人士:没听说过相关新闻:印媒:OPPO计划2024年初在印度推出首款电动汽车新浪科技讯11月22日晚间消息,针对2024年在印度推出电动汽车的传闻,OPPO相关人士回应称,没有听说过。据印度媒体91mobiles报 ...
·《小敏家》钱峰结局 钱峰战小捷最后有正在一起吗
《小敏家》钱峰结局 钱峰战小捷最后有正在一起吗http://upload.mnw.cn/2021/1219/1639919623493.jpg...
·一度火到东南亚,却因爱上2个女人备受争议,林峯成这样,怨谁?
一度火到东南亚,却因爱上2个女人备受争议,林峯成这样,怨谁?报!Wuli“咆哮教主”后继有人了!他,一张口就青筋暴起、口水喷射。他,一激动就抓着女主角的胳膊疯狂摇晃。他,出圈的经典台词有以下这几句:他就是热播电视剧《星辰大海》里的方恒之,一个易燃易爆炸的霸总, ...




Visa称将和亚马逊解决信用卡手续费纠纷:继续在英美市场合作








中国东盟建立全面战略伙伴关系 北京明年将扩大住房供应 | 财经晚6点



友情链接